-
奇数
 奇数
奇数
奇数(外文名:odd number,又名:单数)是整数中不能被2整除的数,可以分为正奇数和负奇数,奇数的个位为1,3,5,7,9,数学表达形式为:2k+1。
目录
- 1 基本信息
2 基本简介
3 性质
4 与平方数
5 与素数
基本信息
中文名:奇数
别称:单数
应用学科:数学
定义:不能被2整除的数
外文名:odd number
表达式:2k+1(k为整数)
适用领域范围:代数
基本简介
 奇数
奇数
正奇数:1、3、5、7、9、11、13、15、17、19、21、23、25、27、29、31、33.........
负奇数:-1、-3、-5、-7、-9、-11、-13、-15、-17、-19、-21、-23.-25、-27、-29、-31、-33.........
性质
关于奇数和偶数,有下面的性质:
(1)两个连续整数中必有一个奇数和一个偶数;
(2)奇数+奇数=偶数;偶数+奇数=奇数;偶数+偶数+...+偶数=偶数;
(3)奇数-奇数=偶数;偶数-奇数=奇数;奇数-偶数=奇数;
(4)若a、b为整数,则a+b与a-b有相同的奇偶性,即a+b与a-b同为奇数或同为偶数;
(5)n个奇数的乘积是奇数,n个偶数的乘积是偶数;算式中有一个是偶数,则乘积是偶数;
(6)奇数的个位是1、3、5、7、9;偶数的个位是0、2、4、6、8;
(7)奇数的平方除以2、4、8余1;
(8) 任意两个奇数的平方差是2、4、8的倍数
(9)奇数除以2余数为1
与平方数
著名数学家毕达哥拉斯发现有趣奇数现象:将奇数连续相加,每次的得数正好是平方数。这体现在奇数和平方数之间有着密切的重要联系。如:
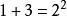
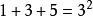
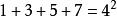
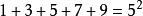
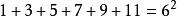
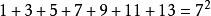
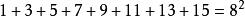
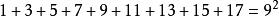

性质:任意一个奇数都可以写成两个整数平方差的形式。
①如1=1²-0²,3=2²-1²,5=3²-2²...
令正奇数a为第n个正奇数(即n≥1),则有a=n²-(n-1)²=2n-1;a=(a+1-n)²-(a-n)²=2a-2n+1.
②如-1=0²-1²,-3=1²-2²,-5=2²-3²...
令负奇数b为第n个负奇数(n≥1),由①改变符号,易得b=-a=(n-1)²-n²=1-2n;
但第二个规律与正奇数的不同。
与素数
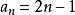 。它有一个优美的性质:n取任何正整数时,它的前n项和均是一个完全平方数,即
。它有一个优美的性质:n取任何正整数时,它的前n项和均是一个完全平方数,即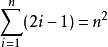
奇数列也可从另一角度进行表述:若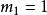 ,
,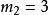 ,当
,当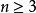 时,都有
时,都有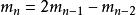 ,则数列
,则数列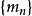 为奇数列。
为奇数列。
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。













