-
正相关
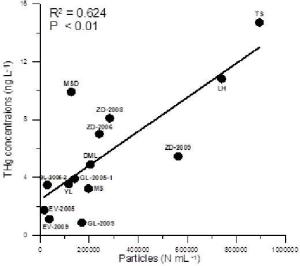 正相关
正相关
正相关是指自变量增长,因变量也跟着增长。两个变量变动方向相同,一个变量由大到小或由小到大变化时,另一个变量亦由大到小或由小到大变化。
目录
- 1 基本信息
2 定义
3 辨析
4 举例
5 正相关的函数
基本信息
中文名:正相关
解释:自变量增长,因变量也跟着增长
适用范围:数理科学
外文名:Positive correlation
对称:负相关
定义
正相关(Positive correlation),是指两个变量变动方向相同,一个变量由大到小或由小到大变化时,另一个变量亦由大到小或由小到大变化。即其数据曲线的切线斜率始终大于零。如身高与体重,身高越长,体重就越重。也就是说,在正相关的情况下,一个变量随着另一个变量的变化而发生相同方向的变化(两个变量同时变大或变小)。其中,引起变化的量叫做自变量(即自己发生变化的量),另一个变量叫做因变量(即跟着自变量变化的量)。
统计学中常用相关系数r来表示两变量之间的相关关系。r的值介于-1与1之间,r为正时是正相关,反映当x增加(减少)时,y随之相应增加(减少);呈正相关的两个变量之间的相关系数一定为正值,这个正值越大说明正相关的程度越高。
当这个正值为1时就是完全正相关的情形,如点子排为一条直线,为完全正相关。正相关虽然意思明确,其实是个模糊的概念,不可以量化,只是定性说法。如果有明确的关系,例如y=2x,这叫y与x成正比,如果只是大体上,x、y的变化方向一样,例如x上升,y也上升或者x下降,y也下降,那么,这叫正相关。反之,x上升,y却下降,或者x下降,y却上升,就叫负相关了。
辨析
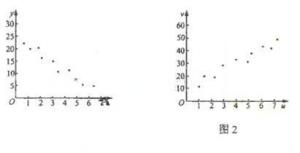
不过日常生活中常说的“正比”多与“正相关”混淆。 例如“收入高低与学历高低成正比”这句话,严格来说是不科学的,因为找不到确定的比例系数k。当然我们都理解这句话的意思是说“学历越高收入则越高”,严格来说应该这样表述:“收入高低与学历高低正相关”。
简而言之,就是有直接的因果关系。
正比,有一个确定的比例系数,如正比例函数:y=2x,比例系数是2,那么,可见,
| x | …… | -1 | 0 | 1 | 2 | 3 | …… |
| y | …… | -2 | 0 | 2 | 4 | 6 |
这样,每当x增加1时,相应的y值就会增加2。这样,每当x减少1时,相应的y值就会减少2。
更准确地说,每当x增加1时,相应的y值就会增加1的2倍。这样,每当x减少1时,相应的y值就会减少1的2倍。
区别
正相关,只是一种概念上的,并且是基于大量的统计数据所展现出来的连个指标间的一种相互关系,而非具体两个个体之间一定满足这样的同向变化关系.有这么一种趋势和相关关系的两个变量,因变量和自变量之间并没有确定的数量关系,即没有很具体和比例系数k。如身高与体重:身高增加,体重一般也会增加,但身高增加一厘米,体重可能增加1斤,也可能是2斤,甚至10斤。所以体重与身高成正相关,而不是成正比。
在函数图形上看,正比表现为直线,有具体的线性关系;正相关则表现为向右上方倾斜的趋势,可以是非线性的。
下图就是典型的非线性正相关。
右图可以看出,途中曲线的数值随x增大y也随着增大,其曲线斜率k始终大于零。
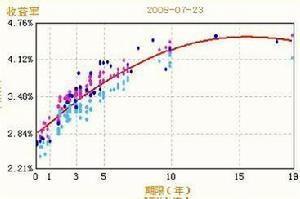 资金收益率和年限的正相关
资金收益率和年限的正相关
举例
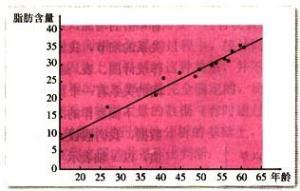
在一次对人体内脂肪含量与年龄关系的研究中,研究人员的出了一组样本数据:
| 年龄 | 23 | 27 | 39 | 41 | 45 | 49 | 50 | 53 | 54 | 56 | 57 | 58 | 60 | 61 |
| 脂肪含量 | 9.5 | 17.8 | 21.2 | 25.9 | 27.5 | 26.3 | 28.2 | 29.6 | 30.2 | 31.4 | 30.8 | 33.5 | 35.2 | 34.6 |
下面便要做出散点图(而不是函数图象),因为从表中可以看到年龄为57的,脂肪含量并没有增大。
对与表中数据,我们假设人的年龄影响体内脂肪含量,于是,按照习惯,以x轴表示年龄,以y轴表示脂肪含量,得到散点图:
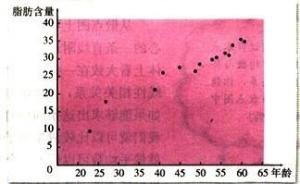
线性回归
附:回归直线的算法: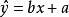
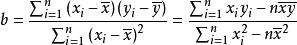
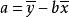
正相关的函数
y=kx+b(k>0)
y=x^a(x>0,a>0)
y=a^x(a>1)
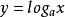
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。













