-
皮尔逊相关系数
在统计学中,皮尔逊相关系数( Pearson correlation coefficient),又称皮尔逊积矩相关系数(Pearson product-moment correlation coefficient,简称PPMCC或PCCs),是用于度量两个变量X和Y之间的相关(线性相关),其值介于-1与1之间。
目录
- 1 基本信息
2 函数介绍
3 定义
4 数学特性
5 解释
6 分析
基本信息
中文名:皮尔逊相关系数
别名:皮尔逊积矩相关系数
学科:统计学
外文名:Pearson correlation coefficient
相关人物:卡尔·皮尔逊;弗朗西斯·高尔顿
函数介绍
皮尔逊相关系数函数是一种用于计算两个变量之间线性相关程度的函数。在数学上,它的公式为:
r = (nΣxy - ΣxΣy) / sqrt((nΣx^2 - (Σx)^2)(nΣy^2 - (Σy)^2))
其中,r表示皮尔逊相关系数,n表示样本数量,x和y分别表示两个变量的取值,Σ表示求和符号。
皮尔逊相关系数函数的输入是两个变量的取值,输出是它们之间的相关系数。通常情况下,相关系数的取值范围在-1到1之间,其中-1表示完全负相关,0表示无相关,1表示完全正相关。在实际应用中,皮尔逊相关系数函数可以用于数据分析、统计建模、机器学习等领域,帮助研究者了解数据之间的关系,从而做出更好的决策。
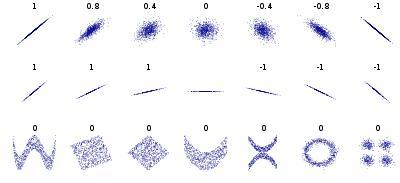
图1中,几组的点集,以及各个点集中
和
之间的相关系数。我们可以发现相关系数反映的是变量之间的线性关系和相关性的方向(第一排),而不是相关性的斜率(中间),也不是各种非线性关系(第三排)。请注意:中间的图中斜率为0,但相关系数是没有意义的,因为此时Y变量是0。
定义
皮尔逊相关系数是一种用于衡量两个变量之间线性相关程度的统计量。它的取值范围在-1到1之间,其中-1表示完全负相关,0表示无相关,1表示完全正相关。皮尔逊相关系数是最常用的相关系数之一,广泛应用于社会科学、自然科学、医学等领域的数据分析中。它可以帮助研究者了解两个变量之间的关系,从而更好地理解数据和现象。皮尔逊相关系数的计算基于两个变量的协方差和标准差,可以通过公式 r = cov(X,Y) / (std(X) * std(Y)) 来计算,其中cov(X,Y)表示X和Y的协方差,std(X)和std(Y)分别表示X和Y的标准差。
数学特性
皮尔逊相关系数具有以下数学特性:
取值范围在-1到1之间,其中-1表示完全负相关,0表示无相关,1表示完全正相关。
如果两个变量之间存在线性关系,则皮尔逊相关系数为正数;如果两个变量之间存在负的线性关系,则皮尔逊相关系数为负数。
皮尔逊相关系数对数据的分布形态有一定要求,即两个变量的分布应该近似于正态分布。
皮尔逊相关系数对异常值比较敏感,如果数据中存在异常值,则可能会导致相关系数的计算结果不准确。
皮尔逊相关系数可以用于衡量两个变量之间的线性关系,但不能用于衡量非线性关系。
皮尔逊相关系数可以通过假设检验来判断两个变量之间的相关性是否显著。
解释
皮尔逊相关系数是用于衡量两个变量之间线性相关程度的统计量。它的取值范围在-1到1之间,其中-1表示完全负相关,0表示无相关,1表示完全正相关。皮尔逊相关系数可以帮助研究者了解两个变量之间的关系,从而更好地理解数据和现象。
例如,如果一个研究者想要了解身高和体重之间的关系,可以使用皮尔逊相关系数来计算它们之间的相关性。如果计算出的相关系数为0.8,那么可以认为身高和体重之间存在较强的正相关关系,即身高越高的人体重也越重。
另外,皮尔逊相关系数还可以用于研究其他变量之间的关系,例如年龄和收入、学历和职业等。通过计算相关系数,研究者可以了解这些变量之间的相关性,从而更好地理解数据和现象,为决策提供支持。
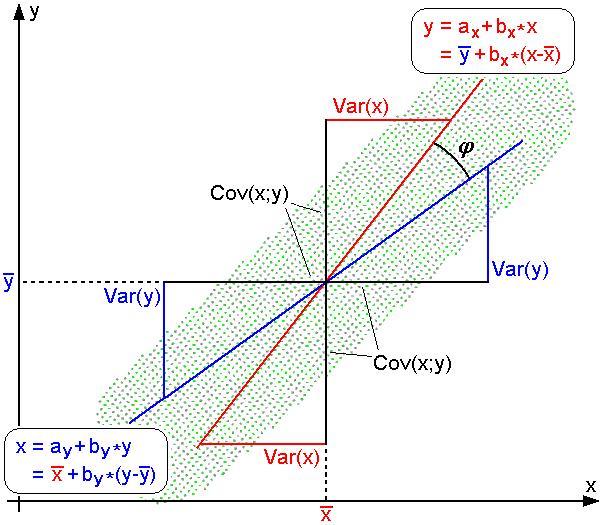
说明:图2中,回归直线: 和
2.皮尔逊距离
皮尔逊距离度量的是两个变量X和Y,它可以根据皮尔逊系数定义成dx,y=1-x,y,我们可以发现,皮尔逊系数落在,而皮尔逊距离落在。
分析
皮尔逊相关系数是用于衡量两个变量之间线性相关程度的统计量。在进行皮尔逊相关系数分析时,通常需要进行以下步骤:
收集数据:收集两个变量的数据,可以使用问卷调查、实验、观察等方法。
检查数据:检查数据是否存在异常值、缺失值等问题,如果存在需要进行数据清洗和处理。
计算相关系数:使用皮尔逊相关系数公式计算两个变量之间的相关系数。
判断相关性:根据相关系数的取值范围,判断两个变量之间的相关性。如果相关系数为正数,则表示两个变量之间存在正相关关系;如果相关系数为负数,则表示两个变量之间存在负相关关系;如果相关系数为0,则表示两个变量之间不存在线性相关关系。
进行假设检验:使用假设检验方法判断相关系数是否显著。通常情况下,如果相关系数的p值小于0.05,则可以认为相关系数是显著的。
进行解释和应用:根据相关系数的取值和显著性,解释两个变量之间的关系,并根据分析结果进行应用和决策。
需要注意的是,皮尔逊相关系数只能用于衡量两个变量之间的线性相关关系,不能用于衡量非线性关系。此外,相关系数的计算结果可能会受到数据分布、样本大小等因素的影响,需要进行综合分析和判断。
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。













