-
平均数
 平均数
平均数
平均数(average)是统计学中最常用的统计量,是表示一组数据集中趋势的量数。
平均数的计算方法是:一组数据中所有数据之和再除以这组数据的个数。用平均数表示一组数据的情况,有直观、简明的特点,所以在日常生活中经常用到,如平均速度、平均身高、平均产量、平均成绩等等。
目录
- 1 基本信息
2 基础定义
3 应用举例
4 类型
5 性质
6 区别联系
基本信息
中文名:平均数
应用领域:统计学
数据:易受到极端数据的影响
外文名:average
学科:数学
分类:算数平均数、几何平均数
基础定义
平均数是统计学中最常用的统计量,用来表明资料中各观测值相对集中较多的中心位置。在畜牧业、水产业生产实践和科学研究中,平均数被广泛用来描述或比较各种技术措施的效果、畜禽某些数量性状的指标等等。
统计平均数是用于反映现象总体的一般水平,或分布的集中趋势。数值平均数是总体标志总量对比总体单位数而计算的。
平均数是统计中的一个重要概念。小学数学里所讲的平均数一般是指算术平均数,也就是一组数据的和除以这组数据的个数所得的商。在统计中算术平均数常用于表示统计对象的一般水平,它是描述数据集中位置的一个统计量。既可以用它来反映一组数据的一般情况、和平均水平,也可以用它进行不同组数据的比较,以看出组与组之间的差别。用平均数表示一组数据的情况,有直观、简明的特点,所以在日常生活中经常用到,如平均速度、平均身高、平均产量、平均成绩等等。
应用举例
解题关键:找准“总数量”相对应的“总分数”
常用方法:作图法、假设法
例题如下:
1、 3头牛和6只羊一天共吃草93千克,6头牛和5只羊一天共吃草130千克。3头牛一天共吃草多少千克?
正解:45千克
直接求法:利用公式求出平均数,这是由“均分”思想产生的方法。
总数量÷总份数=平均数
基数求法:利用公式求平均数。这里是选设各数中最小者为基数,它是由“补差”思想产生的方法。
基数+各数与基数的差÷总份数=平均数
2、:李师傅前4天平均每天加工30个零件,改进技术后,第五天加工零件55个,李师傅5天中平均每天加工多少零件?
解答:先算出5天的总零件数:30×4+55=175(个),再求出5天中平均每天加零件的个数。
(30×4+55)÷5=35(个)
3、 四(1)班有学生40人,数学期末考试时有三位同学困病缺考,平均成绩是80分。后来这三位同学补考,成绩分别为88分、87分和85分,这时全班同学的平均成绩是多少分?
正解:(40—3)×80=2960(分)
(2960+88+87+85)÷40=80.5(分)
4、王师傅4天平均加工26个零件,第5天加工的零件数比5天平均数还多4.8个。王师傅第5天加工多少个零件?
解答:设王师傅第5天加工,x个零件。由5天平均数这个“量”可列方程。
X-4.8=26×4+x)÷5
5x-24=104+x
4x=128
X=32
5、一个学生前六次测验的平均分是93分,比七次测验的平均分高3分,他第七次测验得了多少分?
正解:93×6=558(分) 93—3=90(分) 90×7=630(分)
630—588=72(分)
6、小明前几次数学测验的平均成绩是84分,这一次要考100分才能把平均成绩提高到86分。这一次是第几次测验?
解答:(100-84)÷(86-84)=8次
7、小松前几次考试的平均成绩是84分,这一次考了94分就把平均成绩提高到86分了。这一次是第几次考试?
正解:(94—84) ÷(86—84)=10÷2=5(次)
8、张明前五次数学测验的平均成绩是88分。为了使平均成绩达到92.5分,张明要连续考多少次满分?(每次测验满分是100分。)
解答:(92.5-88)×5÷(100-92.5)=4.5×5÷7.5=3(次)
9、小王前5次数学考试的平均成绩是85.8分,为了使平均成绩尽快达到90分以上,小王至少还要参加几次考试?(每次满分为100分。)
正解:(90—85.8)×5÷(100-90)=4.2×5÷10=2.1
类型
arithmetic mean
算术平均数是指在一组数据中所有数据之和再除以数据的个数。它是反映数据集中趋势的一项指标。
把n个数的总和除以n,所得的商叫做这n个数的算术平均数。
公式: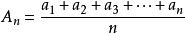
几何平均数
geometric mean
n个观察值连乘积的n次方根就是几何平均数。根据资料的条件不同,几何平均数分为加权和不加权之分。
公式: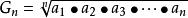
调和平均数
harmonic mean
调和平均数是平均数的一种。但统计调和平均数,与数学调和平均数不同。在数学中调和平均数与算术平均数都是独立的自成体系的。计算结果两者不相同且前者恒小于后者。 因而数学调和平均数定义为:数值倒数的平均数的倒数。但统计加权调和平均数则与之不同,它是加权算术平均数的变形,附属于算术平均数,不能单独成立体系。且计算结果与加权算术平均数完全相等。 主要是用来解决在无法掌握总体单位数(频数)的情况下,只有每组的变量值和相应的标志总量,而需要求得平均数的情况下使用的一种数据方法。
公式: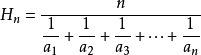
加权平均数
 平均数
平均数
加权平均数是不同比重数据的平均数,加权平均数就是把原始数据按照合理的比例来计算,若 n个数中,x1出现f1次,x2出现f2次,…,xk出现fk次,那么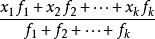 叫做x1、x2、…、xk的加权平均数。f1、f2、…、fk是x1、x2、…、xk的权。
叫做x1、x2、…、xk的加权平均数。f1、f2、…、fk是x1、x2、…、xk的权。
公式: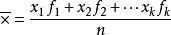 ,其中
,其中 。f1、f2、…、fk叫做权(weight)。
。f1、f2、…、fk叫做权(weight)。
平均数是加权平均数的一种特殊情况,即各项的权相等时,加权平均数就是算术平均数。
平方平均数
平方平均数是n个数据的平方的算术平均数的算术平方根。
公式: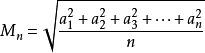
指数平均数
指标概述
指数平均数,其构造原理是对股票收盘价进行算术平均,并根据计算结果来进行分析,用于判断价格未来走势得变动趋势。
EXPMA指标是一种趋向类指标,与平滑异同移动平均线、平行线差指标相比,EXPMA指标由于其计算公式中着重考虑了价格当天 行情得权重,因此在使用中可克服其他指标信号对于价格走势得滞后性。同时也在一定程度中消除了DMA指标在某些时候对于价格走势所产生得信号提前性,是一个非常有效得分析指标。
中位数
中位数(median)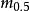 是刻划平均水平的统计量,设
是刻划平均水平的统计量,设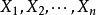 是来自总体的样本,将其从小到大排序为
是来自总体的样本,将其从小到大排序为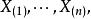 则中位数定义为:
则中位数定义为:
n为奇数时,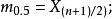
n为偶数时,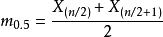
性质
1、样本各观测值与平均数之差的和为零,即离均差之和等于零。
即用公式表示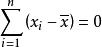
2、样本各观测值与平均数之差的平方和为最小,即离均差平方和为最小。
即用公式表示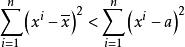
区别联系
平均数、中位数和众数都是来刻画数据平均水平的统计量,它们各有特点。对于平均数大家比较熟悉,中位数刻画了一组数据的中等水平,众数刻画了一组数据中出现次数最多的情况。
平均数非常明显的优点之一是,它能够利用所有数据的特征,而且比较好算。另外,在数学上,平均数是使误差平方和达到最小的统计量,也就是说利用平均数代表数据,可以使二次损失最小。因此,平均数在数学中是一个常用的统计量。但是平均数也有不足之处,正是因为它利用了所有数据的信息,平均数容易受极端数据的影响。例如,在一个单位里,如果经理和副经理工资特别高,就会使得这个单位所有成员工资的平均水平也表现得很高,但事实上,除去经理和副经理之外,剩余所有人的平均工资并不是很高。这时,中位数和众数可能是刻画这个单位所有人员工资平均水平更合理的统计量。中位数和众数这两个统计量的特点都是能够避免极端数据,但缺点是没有完全利用数据所反映出来的信息。由于各个统计量有各自的特征,所以需要我们根据实际问题来选择合适的统计量。
当然,出现极端数据不一定用中位数,一般,统计上有一个方法,就要认为这个数据不是来源于这个总体的,因而把这个数据去掉。比如大家熟悉的跳水比赛评分,为什么要去掉一个最高分、一个最低分呢,就认为这两个分不是来源于这个总体,不能代表裁判的鉴赏力。于是去掉以后再求剩下数据的平均数。需要指出的是,我们处理的数据,大部分是对称的数据,数据符合或者近似符合正态分布。这时候,均值(平均数)、中位数和众数是一样的。
区别
只有在数据分布偏态(不对称)的情况下,才会出现均值、中位数和众数的区别。所以说,如果是正态的话,用哪个统计量都行。如果偏态的情况特别严重的话,可以用中位数。
除了需要刻画平均水平的统计量,统计中还有刻画数据波动情况的统计量。比如,平均数同样是5,它所代表的数据可能是1、3、5、7、9,可能是4、4.5、5、5.5、6。也就是说5所代表的不同组数据的波动情况是不一样的。怎样刻画数据的波动情况呢?很自然的想法就是用最大值减最小值,即求一组数据的极差。数学中还有方差、标准差等许多用来刻画数据特征的统计量。当然这些都是教师感兴趣、值得了解的内容,不是小学数学的教学要求。
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。













