电场力是当电荷置于电场中所受到的作用力，或是在电场中为移动自由电荷所施加的作用力，其大小可由库仑定律得出。电场力的方向为：正电荷沿电场线的切线方向，负电荷沿电场线的切线方向的反方向。

中文名：电场力

提出者：库仑

遵循法则：平行四边形法则

外文名：electric field force

公式：F=qE

单位：牛顿(N)

电荷之间的相互作用是通过电场发生的。只要有电荷存在，电荷的周围就存在着电场。电场的基本性质是它对放入其中的电荷有力的作用，这种力就叫做电场力。电场力是当电荷置于电场中所受到的作用力。或是在电场中为移动自由电荷所施加的作用力。其大小可由库仑定律得出。当有多个电荷同时作用时，其大小及方向遵循矢量运算规则。

电场力

电场方向

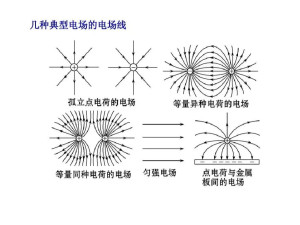
正电荷沿电场线的切线方向，负电荷沿电场线的切线方向的反方向。

大小计算

电场力的计算公式是F=qE，其中q为点电荷的带电量，E为场强。或由W=Fd，也可以根据电场力做功与在电场力方向上运动的距离来求。电磁学中另一个重要公式W=qU（其中U为两点间电势差），就是由此公式推导得出。

相关定律公式

任何电场中适用的公式：静电力F静=qE。

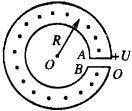
匀强电场通用公式：E=U/d（注：d指两极板的距离，U指两极板电势差）

还有真空中点电荷适用的公式：F=k(Qq/r2) （注：静电力常量k=9.0×109N·m2/C2）

万有引力公式：F=G(Mm/r2) （注：万有引力常量G=6.67×10-11N·m2/kg2）

由于电场力的作用广泛，它应用到粒子加速器、航天事业中导航修正、对新物质的加工、改变物质内部粒子的排列等等，在未来可能是工程与技术的主要动力之一。

应用前景

在未来有电场力的存在航空航天事业会得到长足发展，例如利用电场保护层（可以让飞行器更轻）；以及让飞行器依赖电场飞行（而取代现有的发动机）；电场在核物质的衰变起作用（让我们能更好的利用能源）。

判断电势高低的方法

电场具有力的性质和能的性质，描述电场的物理量有电势、电势能、静电力、静电力做功等，为了更好地描述电场，还有电场线、等势面等概念，可以从多个角度判断电势高低。

1、利用电场线判断电势高低．沿电场线的方向电势越来越低。

2、在正电荷产生的电场中，离电荷越近电势越高，在负电荷产生的电场中，离电荷越近，电势越低。

3、电势的正负．若以无穷远处电势为零，则正点电荷周围各点电势为正，负点电荷周围各点电势为负。

4、根据只在静电力作用下电荷的移动情况来判断。只在静电力作用下，电荷由静止开始移动，正电荷总是由电势高的点移向电势低的点；负电荷总是由电势低的点移向电势高的点。但它们都是由电势能高的点移向电势能低的点。

1785年，库仑用自己发明的扭秤建立了静电学中著名的库仑定律。同年，他在给法国科学院的《电力定律》的论文中详细地介绍了他的实验装置、测试经过和实验结果。

证明方法

库仑的扭秤是由一根悬挂在细长线上的轻棒和在轻棒两端附着的两只平衡球构成的。当球上没有力作用时，棒取一定的平衡位置。如果两球中有一个带电，同时把另一个带同种电荷的小球放在它附近，则会有电力作用在这个球上，球可以移动，使棒绕着悬挂点转动，直到悬线的扭力与电的作用力达到平衡时为止。因为悬线很细，很小的力作用在球上就能使棒显著地偏离其原来位置，转动的角度与力的大小成正比。库仑让这个可移动球和固定的球带上不同量的电荷，并改变它们之间的距离：

第一次，两球相距36个刻度，测得银线的旋转角度为36度。

第二次，两球相距18个刻度，测得银线的旋转角度为144度。

第三次，两球相距8.5个刻度，测得银线的旋转角度为575.5度。

上述实验表明，两个电荷之间的距离为4：2：1时，扭转角为1：4：16。由于扭转角的大小与扭力成反比，所以得到：两电荷间的斥力的大小与距离的平方成反比。库仑认为第三次的偏差是由漏电所致。

经过了这们巧妙的安排，仔细实验，反复的测量，并对实验结果进行分析，找出误差产生的原因，进行修正，库仑终于测定了带等量同种电荷的小球之间的斥力。

但是对于异种电荷之间的引力，用扭秤来测量就遇到了麻烦。因为金属丝的扭转的回复力矩仅与角度的一次方成比例，这就不能保证扭称的稳定。经过反复的思考，库仑发明了电摆。他利用与单摆相类似的方法测定了异种电荷之间的引力也与它们的距离的平方成反比。

最后库仑终于找出了在真空中两个点电荷之间的相互作用力与两点电荷所带的电量及它们之间的距离的定量关系，这就是静电学中的库仑定律，即两电荷间的力与两电荷的乘积成正比，与两者的距离平方成反比。库仑定律是电学发展史上的第一个定量规律，它使电学的研究从定性进入定量阶段，是电学史中的一块重要的里程碑。电荷的单位库仑就是以他的姓氏命名的。

相关理论

磁学中的库仑定律也是利用类似的方法得到的。1789年法国大革命爆发，库仑隐居在自己的领地里，每天全身心地投入到科学研究的工作中去。同年，他的一部重要著作问世，在这部书里，他对有两种形式的电的认识发展到磁学理论方面，并归纳出类似于两个点电荷相互作用的两个磁极相互作用定律。库仑以自己一系列的著作丰富了电学与磁学研究的计量方法，将牛顿的力学原理扩展到电学与磁学中。库仑的研究为电磁学的发展、电磁场理论的建立开拓了道路。这是他的扭秤在精密测量仪器及物理学的其它方面也得到了广泛的应用。

库仑不仅在力学和电学上都做出了重大的贡献。做为一名工程师，他在工程方面也作出过重要的贡献。他曾设计了一种水下作业法。这种作业法类似于现代的沉箱，它是应用在桥梁等水下建筑施工中的一种很重要的方法。

库仑（Charlse-Augustin de Coulomb，1736 --1806），法国工程师、物理学家。1736年6月14日生于法国昂古莱姆。1806年8月23日在巴黎逝世。早年就读于美西也尔工程学校。离开学校后，进入皇家军事工程队当工程师。法国大革命时期，库仑辞去一切职务，到布卢瓦致力于科学研究。法皇执政统治期间，回到巴黎成为新建的研究院成员。1773年发表有关材料强度的论文，所提出的计算物体上应力和应变分布情况的方法沿用，是结构工程的理论基础。1777年开始研究静电和磁力问题。当时法国科学院悬赏征求改良航海指南针中的磁针问题。库仑认为磁针支架在轴上，必然会带来摩擦，提出用细头发丝或丝线悬挂磁针。研究中发现线扭转时的扭力和针转过的角度成比例关系，从而可利用这种装置测出静电力和磁力的大小，这导致他发明扭秤。他还根据丝线或金属细丝扭转时扭力和指针转过的角度成正比，因而确立了弹性扭转定律。他根据1779年对摩擦力进行分析，提出有关润滑剂的科学理论，于1881年发现了摩擦力与压力的关系，表述出摩擦定律、滚动定律和滑动定律。设计出水下作业法，类似现代的沉箱。1785~1789年，用扭秤测量静电力和磁力，导出著名的库仑定律。库仑定律使电磁学的研究从定性进入定量阶段，是电磁学史上一块重要的里程碑。