-
圆锥
 圆锥
圆锥
圆锥是一种几何图形,有两种定义。解析几何定义:圆锥面和一个截它的平面(满足交线为圆)组成的空间几何图形叫圆锥。立体几何定义:以直角三角形的直角边所在直线为旋转轴,其余两边旋转360度而成的曲面所围成的几何体叫做圆锥。
目录
- 1 基本信息
2 基础定义
3 应用举例
4 演绎过程
5 组成
6 测量
基本信息
中文名:圆锥
体积公式:底面积×高×1/3 V锥=1/3sh
分类:数学
外文名:circular cone
表面积公式:侧面积+底面积
属于:几何图形
基础定义
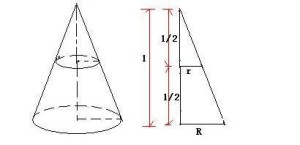 圆锥
圆锥
以直角三角形的直角边所在直线为旋转轴,其余两边旋转而成的曲面所围成的几何体叫做圆锥。
注意:圆锥不是特殊的圆柱。
应用举例
生活中沙堆、漏斗、帽子、陀螺、斗笠、铅笔头、钻头、铅锤等都可以近似地看作圆锥。圆锥在日常生活中也是不可或缺的。
演绎过程
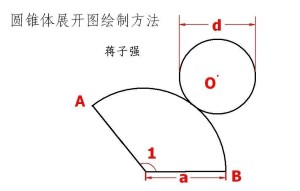 展开图
展开图
∵弧AB=⊙O的周长
∴弧AB=πd
∵弧AB=2πa(∠1/360°)
∴2πa(∠1/360°)=πd
∴2a(∠1/360°)=d
将a,d带入2a(∠1/360°)=d得到∠1的值。这样绘制展开图的所有所需数据都求出来了。根据数据即可画出圆锥的展开图。
母线长等于底面圆直径的圆锥,展开的扇形就是半圆。所有圆锥展开的扇形角度等于(底面直径÷母线)×180度。
三视图
圆锥三视图是观测者从三个不同位置观察而画出的图形。
其主视图和侧视图均为等腰三角形,俯视图是一个圆和圆心。
组成
 圆锥
圆锥
圆锥母线:圆锥的侧面展开形成的扇形的半径、底面圆周上任意一点到顶点的距离。
圆锥的侧面积:将圆锥的侧面沿母线展开,是一个扇形,这个扇形的弧长等于圆锥底面的周长,而扇形的半径等于圆锥的母线的长. 圆锥的侧面积就是弧长为圆锥底面的周长×母线/2;没展开时是一个曲面。
圆锥有一个底面、一个侧面、一个顶点、一条高、无数条母线,且底面展开图为一圆形,侧面展开图是扇形。
测量
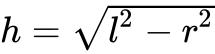
底面周长
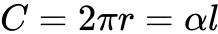
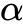 :侧面展开图圆心角弧度,l:母线长)
:侧面展开图圆心角弧度,l:母线长)表面积
一个圆锥表面的面积叫做这个圆锥的表面积.
圆锥的表面积由侧面积和底面积两部分组成。全面积(S)=S侧+S底
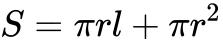
其中,S侧=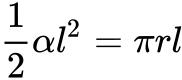 (r:底面半径,l:圆锥母线,
(r:底面半径,l:圆锥母线,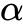 :侧面展开图圆心角弧度)
:侧面展开图圆心角弧度)
体积
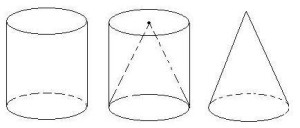 圆锥
圆锥
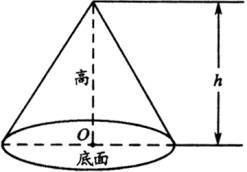
一个圆锥所占空间的大小,叫做这个圆锥的体积。
一个圆锥的体积等于与它等底等高的圆柱的体积的1/3。
根据圆柱体积公式V=Sh(V=πr^2h),得出圆锥体积公式: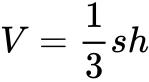 ,其中S是圆柱的底面积,h是圆柱的高,r是圆柱的底面半径。
,其中S是圆柱的底面积,h是圆柱的高,r是圆柱的底面半径。
【证明】
把圆锥沿高分成k份,每份高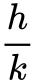 ,
,
第 n份半径: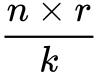
第 n份底面积: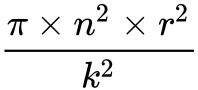
第 n份体积: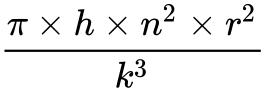
总体积: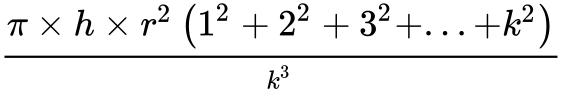
∵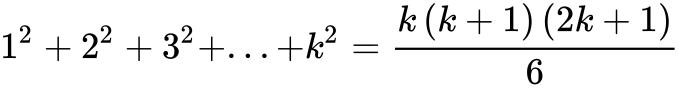
 圆锥
圆锥
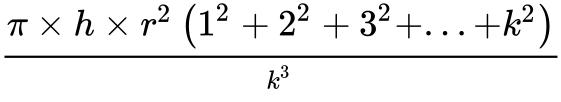
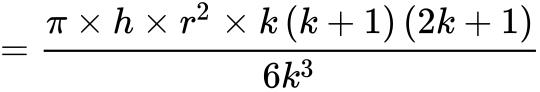
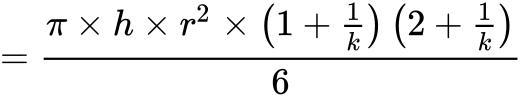
∵ 当k越来越大,总体积越接近于圆锥体积,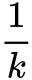 越接近于0
越接近于0
∴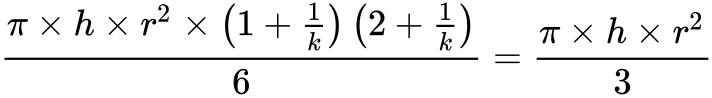
∵ V圆柱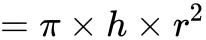
∴ V圆锥是与它等底等高的V圆柱体积的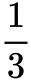
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。













