-
三角形
 三角形
三角形
三角形是由同一平面内不在同一直线上的三条线段首尾顺次连接所组成的封闭图形,为几何图案的基本图形。
三角形按边分有普通三角形(三条边都不相等)、等腰三角形(腰与底不等的等腰三角形、腰与底相等的等腰三角形即等边三角形);按角分有直角三角形、锐角三角形、钝角三角形等。
目录
- 1 基本信息
2 基本定义
3 分类
4 周长公式
5 面积公式
6 四线
7 性质
8 四线
9 性质
10 边角关系
11 全等三角形
12 相似三角形
13 特殊点线
14 有关定理
基本信息
中文名:三角形
学科:数学
分类方法:边、角
外文名:ZiMintion;triangle
包括:锐角、钝角、直角
定义:三条线段首尾顺次连接的图形
基本定义
由不在同一直线上的三条线段首尾顺次连接所组成的封闭图形叫作三角形。平面上三条直线或球面上三条弧线所围成的图形,三条直线所围成的图形叫平面三角形;三条弧线所围成的图形叫球面三角形,也叫三边形。
 三角形
三角形
分类
判定法一:
1、锐角三角形:三角形的三个内角都小于90度。
2、直角三角形:三角形的三个内角中一个角等于90度,可记作Rt△。
3、钝角三角形:三角形的三个内角中有一个角大于90度。
判定法二:
1、锐角三角形:三角形的三个内角中最大角小于90度。
2、直角三角形:三角形的三个内角中最大角等于90度。
3、钝角三角形:三角形的三个内角中最大角大于90度,小于180度。
其中锐角三角形和钝角三角形统称为斜三角形。
判断方法
由余弦定理延伸而来。
若一个三角形的三边a,b,c (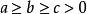 ) 满足:
) 满足:
1、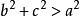 ,则这个三角形是锐角三角形;
,则这个三角形是锐角三角形;
2、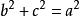 ,则这个三角形是直角三角形;
,则这个三角形是直角三角形;
3、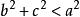 ,则这个三角形是钝角三角形。
,则这个三角形是钝角三角形。
按边分
1、不等边三角形;不等边三角形,数学定义,指的是三条边都不相等的三角形叫不等边三角形。
2、等腰三角形;等腰三角形(isosceles triangle),指两边相等的三角形,相等的两个边称为这个三角形的腰。等腰三角形中,相等的两条边称为这个三角形的腰,另一边叫做底边。两腰的夹角叫做顶角,腰和底边的夹角叫做底角。等腰三角形的两个底角度数相等(简写成“等边对等角”)。等腰三角形的顶角的平分线,底边上的中线,底边上的高重合(简写成“等腰三角形的三线合一性质”)。等腰三角形的两底角的平分线相等(两条腰上的中线相等,两条腰上的高相等)。等腰三角形底边上的垂直平分线到两条腰的距离相等。等腰三角形的一腰上的高与底边的夹角等于顶角的一半。等腰三角形底边上任意一点到两腰距离之和等于一腰上的高(需用等面积法证明)。等腰三角形是轴对称图形,(不是等边三角形的情况下)只有一条对称轴,顶角平分线所在的直线是它的对称轴,等边三角形有三条对称轴。等腰三角形中腰的平方等于高的平方加底的一半的平方。等腰三角形的腰与它的高的关系,直接的关系是:腰大于高。间接的关系是:腰的平方等于高的平方加底的一半的平方。
3、等边三角形。等边三角形(又称正三角形),为三边相等的三角形,其三个内角相等,均为60°,它是锐角三角形的一种。等边三角形也是最稳定的结构。等边三角形是特殊的等腰三角形,所以等边三角形拥有等腰三角形的一切性质。
周长公式
若一个三角形的三边分别为a、b、c,则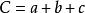 。
。
面积公式
1、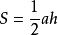 (面积=底×高÷2。其中,a是三角形的底,h是底所对应的高)注释:三边均可为底,应理解为:三边与之对应的高的积的一半是三角形的面积。这是面积法求线段长度的基础。
(面积=底×高÷2。其中,a是三角形的底,h是底所对应的高)注释:三边均可为底,应理解为:三边与之对应的高的积的一半是三角形的面积。这是面积法求线段长度的基础。
2、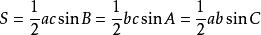 (其中,三个角为∠A,∠B,∠C,对边分别为a,b,c。参见三角函数)
(其中,三个角为∠A,∠B,∠C,对边分别为a,b,c。参见三角函数)
3、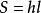 (l为高所在边中位线)
(l为高所在边中位线)
4、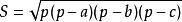 (海伦公式),其中
(海伦公式),其中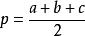
5、秦九韶公式(与海伦公式等价)
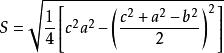
6、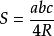 (其中,R是外接圆半径)
(其中,R是外接圆半径)
7、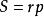 (其中,r是内切圆半径,p是半周长)
(其中,r是内切圆半径,p是半周长)
、在平面直角坐标系内,A(a,b),B(c,d),C(e,f)构成之三角形面积为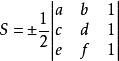 。A,B,C三点最好按逆时针顺序从右上角开始取,因为这样取得出的结果一般都为正值,如果不按这个规则取,可能会得到负值,但只要取绝对值就可以了,不会影响三角形面积的大小。
。A,B,C三点最好按逆时针顺序从右上角开始取,因为这样取得出的结果一般都为正值,如果不按这个规则取,可能会得到负值,但只要取绝对值就可以了,不会影响三角形面积的大小。
9、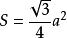 (正三角形面积公式,a是三角形的边长)
(正三角形面积公式,a是三角形的边长)
10、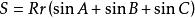 (其中,R是外接圆半径;r是内切圆半径)
(其中,R是外接圆半径;r是内切圆半径)
11、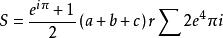
12、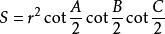
13、设三角形三边为AC,BC,AB,点D垂直于AB,为三角形ABC的高由于DB=BC*cosB, cosB可用余弦定理式表示。
利用余弦定理求得:再利用勾股定理求得CD再用面积=底×高÷2,最终得出面积公式。
四线
连接三角形的一个顶点及其对边中点的线段叫做三角形的中线(median)。
高
从一个顶点向它的对边所在的直线画垂线,顶点和垂足之间的线段叫做三角形的高(altitude)。
角平分线
三角形一个内角的平分线与这个角的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线(bisector of angle)。
中位线
三角形的三边中任意两边中点的连线叫中位线。它平行于第三边且等于第三边的一半。切记,中位线没有逆定理。
性质

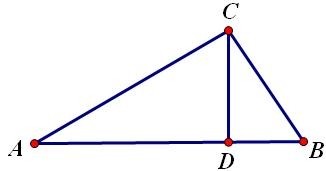
利用余弦定理求得:再利用勾股定理求得CD再用面积=底×高÷2,最终得出面积公式。
四线
连接三角形的一个顶点及其对边中点的线段叫做三角形的中线(median)。
高
从一个顶点向它的对边所在的直线画垂线,顶点和垂足之间的线段叫做三角形的高(altitude)。
角平分线
三角形一个内角的平分线与这个角的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线(bisector of angle)。
中位线
三角形的三边中任意两边中点的连线叫中位线。它平行于第三边且等于第三边的一半。切记,中位线没有逆定理。
性质
 三角形
三角形
2 、在平面上三角形的外角和等于360° (外角和定理)。
3、 在平面上三角形的外角等于与其不相邻的两个内角之和。
推论:三角形的一个外角大于任何一个和它不相邻的内角。
4、 一个三角形的三个内角中最少有两个锐角。
5、 在三角形中至少有一个角大于等于60度,也至少有一个角小于等于60度。
6 、三角形任意两边之和大于第三边,任意两边之差小于第三边。
7、 在一个直角三角形中,若一个角等于30度,则30度角所对的直角边是斜边的一半。
8、直角三角形的两条直角边的平方和等于斜边的平方(勾股定理)。
*勾股定理逆定理:如果三角形的三边长a,b,c满足a²+b²=c² ,那么这个三角形是直角三角形。
9、直角三角形斜边的中线等于斜边的一半。
10、三角形的三条角平分线交于一点,三条高线的所在直线交于一点,三条中线交于一点。
11、三角形三条中线的长度的平方和等于它的三边的长度平方和的3/4。
12、 等底同高的三角形面积相等。
1、3 底相等的三角形的面积之比等于其高之比,高相等的三角形的面积之比等于其底之比。
14、三角形的任意一条中线将这个三角形分为两个面积相等的三角形。
15、等腰三角形顶角的角平分线和底边上的高、底边上的中线在一条直线上(三线合一)。
16、 在同一个三角形内,大边对大角,大角对大边。
在三角形中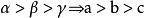 ,其中角α,β,γ分别对着边a,b,c。
,其中角α,β,γ分别对着边a,b,c。
17、 在斜△ABC中恒满足: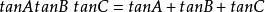 。
。
18、△ABC中恒有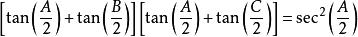 。
。
19、三角形具有稳定性。
边角关系
三角函数给出了直角三角形中边和角的关系,可以用来解三角形。
三角函数是数学中属于初等函数中超越函数的一类。
全等三角形
两个能够完全重合的三角形称为全等三角形。
全等三角形特点
全等三角形的对应角相等,对应边也相等。翻折,平移,旋转,多种变换叠加后仍全等。
全等三角形判定
1、两个三角形对应的三条边相等,两个三角形全等,简称“边边边”或“SSS";
2、两个三角形对应的两边及其夹角相等,两个三角形全等,简称“边角边”或“SAS”;
3、两个三角形对应的两角及其夹边相等,两个三角形全等,简称“角边角”或“ASA”;
4、两个三角形对应的两角及其一角的对边相等,两个三角形全等,简称“角角边”或“AAS”;
5、两个直角三角形对应的一条斜边和一条直角边相等,两个直角三角形全等,简称“斜边、直角边”或“HL”;
注:“边边角”即“SSA”和“角角角”即:"AAA"是错误的证明方法。
相似三角形
对应边成比例的两个三角形叫做相似三角形。
相似三角形性质
1、相似三角形对应边成比例,对应角相等。
2、相似三角形对应边的比叫做相似比。
3、相似三角形的周长比等于相似比,面积比等于相似比的平方。
4、相似三角形对应线段(角平分线、中线、高)之比等于相似比。
相似三角形判定
1、如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似(简称:三边对应成比例的两个三角形相似)。
2、如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似(简称:两边对应成比例且其夹角相等的两三角形相似)。
3、如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似(简称:两角对应相等的两三角形相似)。
4、如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个三角形相似。
特殊点线
五心、四圆、三点、一线:这些是三角形的全部特殊点,以及基于这些特殊点的相关几何图形。“五心”指重心、垂心、内心、外心和旁心;“四圆”为内切圆、外接圆、旁切圆和欧拉圆;“三点”是勒莫恩点、奈格尔点和欧拉点;“一线”即欧拉线。
五心的距离
- OH²=9R²–(a²+b²+c²)。
- OG²=R²–(a²+b²+c²)/9。
- OI²=R²–abc/(a+b+c)=R² – 2Rr。
- GH²=4OG²。
- GI²=(p²+5r²–16Rr)/9。
- HI²=4R²-p²+3r²+4Rr=4R²+2r²-(a²+b²+c²)/2。
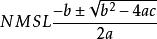
证明
任取三角形两条边,则两条边的非公共端点被第三条边连接。
∴第三条边不可伸缩或弯折
∴两端点距离固定
∴这两条边的夹角固定
∵这两条边是任取的
∴三角形三个角都固定,进而将三角形固定
∴三角形有稳定性
任取n边形(n≥4)两条相邻边,则两条边的非公共端点被不止一条边连接
∴两端点距离不固定
∴这两边夹角不固定
∴n边形(n≥4)每个角都不固定
∴n边形(n≥4)没有稳定性
证毕。
作用
三角形的稳定性使其不像四边形那样易于变形,有着稳定、坚固、耐压的特点。三角形的结构在工程上有
着广泛的应用。许多建筑都是三角形的结构,如:埃菲尔铁塔,埃及金字塔等等。
有关定理
- 中位线定理
- 中线定理
- 三角形内角和定理
- 三边关系定理
- 勾股定理
- 射影定理
- 正弦定理
- 余弦定理
- 正切定理
- 余切定理
- 正割定理
- 余割定理
- 梅涅劳斯定理
- 塞瓦定理
- 莫利定理
- 共角定理
- 重心定理
- 内心定理
- 旁心定理
- 欧拉线定理
- 费尔巴哈定理
- 拿破仑定理
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。













