-
脐点
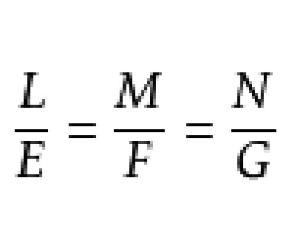 脐点
脐点
若曲面上的一点P,其第一、二基本形式成比例,则称P点为曲面的脐点(umbilical point)。若第二基本形式为零,则称为平点,否则称为圆点。在脐点处总曲率K=H。
目录
- 1 基本信息
2 基本介绍
3 法曲率与脐点
基本信息
中文名:脐点
分类:圆点、平点
所属学科:数学(微分几何学)
外文名:umbilical point
相关概念:法曲率,第一、二基本量/形式等
基本介绍
脐点(umbilical point)是曲面上的一类特殊点,它是第一基本形式与第二基本形式成比例的点,若曲面在某一点处的第一、二类基本量适合
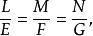
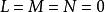 的脐点称为平点,
的脐点称为平点,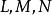 不全为零的脐点称为圆点,平面上的点都是平点,球面上的点都是圆点。
不全为零的脐点称为圆点,平面上的点都是平点,球面上的点都是圆点。法曲率与脐点
法曲率是曲面理论的一个核心概念。
设
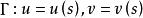
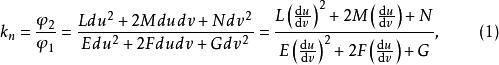
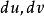 不能同时为零,故不妨在(1)中设
不能同时为零,故不妨在(1)中设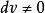 ,这表明法曲率是方向
,这表明法曲率是方向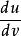 的函数,一般的说不同方向上
的函数,一般的说不同方向上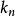 的值也不相同。所谓脐点,就是指曲面上这样一种特殊的点,它的任何方向的
的值也不相同。所谓脐点,就是指曲面上这样一种特殊的点,它的任何方向的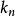 恒为常数。
恒为常数。于是对于脐点,(1)式中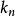 为常数,且对任何方向都成立,自然对于参数曲线方向亦成立,对
为常数,且对任何方向都成立,自然对于参数曲线方向亦成立,对 线显然有
线显然有
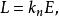
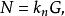
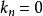 时,由上述两式可直接得到
时,由上述两式可直接得到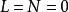 ,再代入(1)式便知
,再代入(1)式便知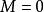 。至于
。至于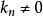 时,则将两式代入(1)式有
时,则将两式代入(1)式有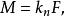
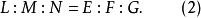
反之,若(2)式成立,则当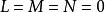 时,显然对任何方向均有
时,显然对任何方向均有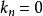 。若
。若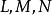 不全为零,不妨设
不全为零,不妨设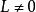 ,于是令
,于是令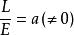 ,则有
,则有
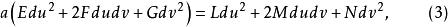
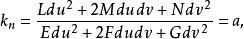
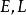 为定值,故
为定值,故 为常数。于是有:
为常数。于是有:定理曲面上一点为脐点的充要条件是
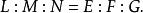
由上述定理的证明过程可以看到,平点是脐点中的一种。
我们又称L、M、N不全为零的脐点为圆点。球面上的点皆为圆点,而且可以证明其逆也成立,从而有:一个曲面为球面或球面一部分的充要条件是其上的每一点都是圆点。对于圆点,如上不妨令
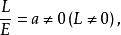
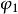 为恒正齐式,即得
为恒正齐式,即得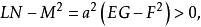
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。













